Fonction W Lambert en calorifugeage : une redécouverte mathématique
Introduction
La fonction W de Lambert est un outil mathématique puissant pour le calcul d’épaisseurs d’isolation thermique dans le calorifugeage. Redécouverte dans les années 1990, cette fonction permet de résoudre analytiquement les équations de transfert thermique qui étaient auparavant traitées par méthodes itératives approximatives. Elle est primordiale dans les calculs d’épaisseurs d’isolation sur tuyauteries.
Histoire et redécouverte
Les origines historiques
La fonction W de Lambert tire son nom de Johann Heinrich Lambert (1728-1777), mathématicien et physicien suisse-allemand qui l’a introduite en 1758 dans ses travaux sur les équations transcendantes. Paradoxalement, malgré son importance théorique, cette fonction est restée largement dans l’ombre pendant plus de deux siècles.
Lambert s’intéressait à la résolution d’équations de la forme \(x = a^x\), et il a découvert que la solution pouvait être exprimée en termes de ce qui est aujourd’hui appelé la fonction W de Lambert. Cependant, les outils de calcul de l’époque ne permettaient pas une exploitation pratique de cette découverte.

La renaissance des années 1990
La véritable renaissance de la fonction W de Lambert débute en 1993 avec les travaux de Robert M. Corless, Gaston H. Gonnet, David E. G. Hare, David J. Jeffrey et Donald E. Knuth. Leur article fondateur « On the Lambert W function » publié dans Advances in Computational Mathematics a non seulement remis cette fonction au goût du jour, mais a également développé les méthodes numériques nécessaires à son calcul pratique.
Cette redécouverte coïncide avec l’essor de l’informatique scientifique et des logiciels de calcul symbolique, rendant enfin accessible ce qui était auparavant purement théorique.
Définition mathématique
Rappel sur la fonction exponentielle
Avant d’aborder la fonction W de Lambert, il convient de rappeler les différentes représentations de la fonction exponentielle, élément central de notre étude.
La fonction exponentielle \(\mathrm{e}^x\) ou \(\exp(x)\) peut être définie de plusieurs manières équivalentes :
Définition par série entière :
$$\mathrm{e}^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots$$
Définition par limite :
$$\mathrm{e}^x = \lim_{n \to \infty} (1 + \frac{x}{n})^n$$
Définition différentielle : La fonction exponentielle est l’unique solution de l’équation différentielle \(y’ = y\) avec la condition initiale \(y(0) = 1\).
Propriétés fondamentales :
- \(\exp(a+b) = \exp(a) \cdot \exp(b)\) (propriété multiplicative)
- \(\frac{\mathrm{d}}{\mathrm{d}x} \exp(x) = \exp(x)\) (dérivée égale à elle-même)
- \(\int \exp(x) \cdot \mathrm{d}x = \exp(x) + C\) (primitive égale à elle-même)
- \(\exp(0) = 1\) et \(\exp(1) = \mathrm{e} \approx 2,71828…\)
- \(\frac{1}{\mathrm{e}} = \mathrm{e}^{-1} = \exp(-1) \approx 0,3679…\)
Ces représentations multiples de la fonction exponentielle sont cruciales pour comprendre la complexité de sa fonction inverse généralisée, la fonction W de Lambert.
Définition fondamentale
La fonction \(\mathrm{W}\) de Lambert est définie comme la fonction inverse de \(f(w) = w \cdot \exp(w)\). Autrement dit, si \(y = w \cdot \exp(w)\), alors \(w = \mathrm{W}(y)\).
Par définition, la fonction \(\mathrm{W}\) satisfait l’équation fondamentale :
$$x = \mathrm{W}(x) \cdot \exp(\mathrm{W}(x))$$
La fonction W Lambert en calorifugeage représente aujourd’hui un outil indispensable pour les ingénieurs thermiciens. Elle permet de résoudre analytiquement les équations qui apparaissent dans le dimensionnement des systèmes d’isolation thermique.
Domaine et branches
La fonction W de Lambert possède deux branches principales :
- \(\mathrm{W}_0(x)\) : la branche principale, définie pour \(x \ge \ – \exp(-1)\)
- \(\mathrm{W}_{-1}(x)\) : la branche secondaire, définie pour \(- \exp(-1) \le x < 0\)
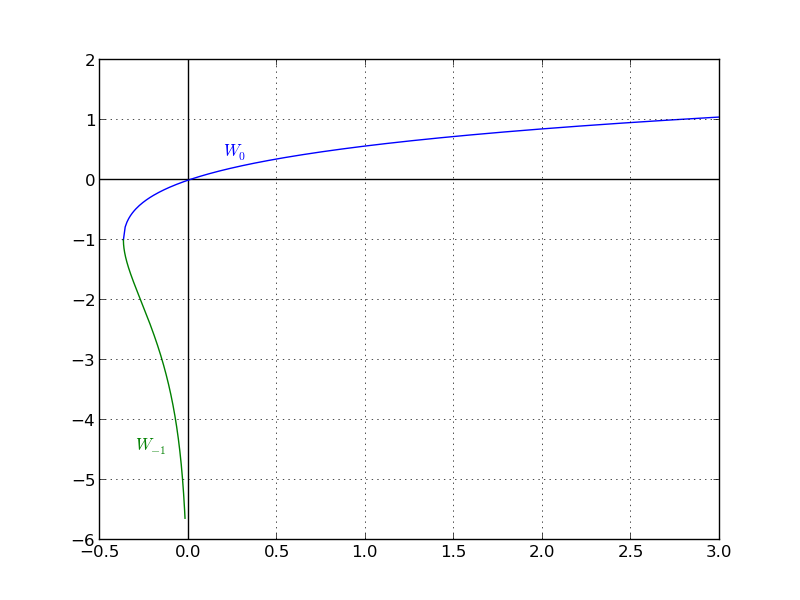
Crédit : Stephan Kulla, CC BY 3.0, via Wikimedia Commons
Le point critique \(x = -\exp(-1) \approx -0,3679\) correspond au minimum de la fonction \(f(w) = w \cdot \exp(w)\), où les deux branches se rejoignent avec \(\mathrm{W}_0(-\exp(-1)) = \mathrm{W}_{-1}(-\exp(-1)) = -1\).
Propriétés remarquables
Quelques valeurs particulières utiles :
- \(\mathrm{W}_0(0) = 0\)
- \(\mathrm{W}_0(\mathrm{e}) = 1\)
- \(\mathrm{W}_0(-\exp(-1)) = \mathrm{W}_{-1}(-\exp(-1)) = -1\)
Comportement asymptotique
Pour les grandes valeurs de \(x\), la fonction W de Lambert présente un comportement asymptotique remarquable :
- \(\mathrm{W}_0(x) \approx \ln(x) – \ln(\ln(x))\) quand \(x \to + \infty\)
- \(\mathrm{W}_{-1}(x) \approx \ln(-x) – \ln(-\ln(-x))\) quand \(x \to 0^{-}\)
Application de la fonction W Lambert en Calorifugeage
Contexte des calculs d’isolation
L’application de la fonction W Lambert en calorifugeage transforme des calculs complexes en solutions directes. Que ce soit pour des tuyauteries cylindriques ou des accessoires toriques, cette fonction permet d’obtenir des résultats précis et conformes aux normes en vigueur.
Types d’exigences courantes
Les calculs d’isolation sont typiquement dimensionnés selon plusieurs critères :
Exigences de température de surface :
- Limitation de la température de surface extérieure (sécurité du personnel, confort)
- Maintien d’une température minimale (anti-condensation, protection antigel)
Conformité aux classes d’isolation normatives :
- Norme EN 12828 : isolation des équipements hydrauliques dans les bâtiments
- Norme EN 17956 : isolation thermique des installations industrielles
Exigences de performance thermique :
- Valeur maximale de résistance thermique (m²·K/W)
- Limitation du coefficient de transmission thermique U (W/m²·K ou W/m·K)
- Respect d’une déperdition thermique linéique maximale (W/m)
- Contrôle des déperditions surfaciques (W/m²)
Équations de transfert thermique
Voir la page Formules de calcul.
Intervention de la fonction W de Lambert
Épaisseur optimisée
Lorsqu’on optimise l’épaisseur d’isolation en tenant compte des coûts énergétiques et des coûts d’investissement, on aboutit à des équations de la forme :
$$D_e \cdot \exp(\frac{D_e}{k}) = C$$
Où \(k\) est un paramètre thermique caractéristique du système, et \(C\) une constante.
La solution de cette équation transcendante s’exprime directement avec la fonction W de Lambert :
$$D_e = k \cdot \mathrm{W}(\frac{C}{k})$$
Calcul d’épaisseurs suivant exigences
Voir la page Épaisseurs sur tuyauteries.
Avantages pratiques
L’utilisation de la fonction W Lambert en calorifugeage dans ces calculs présente plusieurs avantages :
- Conformité rigoureuse : Respect exact des exigences normatives sans approximation
- Rapidité de calcul : Solution directe, particulièrement utile pour le dimensionnement de nombreuses configurations
- Fiabilité : Évite les problèmes de convergence des méthodes itératives classiques
- Automatisation : Facilite l’implémentation dans les outils de calcul
Application aux coudes toriques
Pour les coudes toriques, la géométrie plus complexe introduit des facteurs de forme additionnels, mais le principe reste identique. Les équations de transfert thermique conduisent à des expressions où la fonction W de Lambert permet de résoudre analytiquement le calcul d’épaisseur d’isolation.
Calcul Numérique de la fonction W de Lambert
Algorithmes disponibles
Plusieurs méthodes permettent le calcul numérique de la fonction W de Lambert :
- Méthode de Newton-Raphson
- Développements en série : Utiles au voisinage de points particuliers
- Approximations asymptotiques : Pour les grandes valeurs
Implémentation pratique
La plupart des logiciels de calcul scientifique modernes (MATLAB, Python avec SciPy, Mathematica, etc.) incluent des implémentations optimisées de la fonction W de Lambert, rendant son utilisation aussi simple que celle des fonctions logarithmiques ou exponentielles classiques.
Ci-dessous, un calculateur simple de la fonction W de Lambert.
Calculateur W de Lambert
Questions fréquentes sur la fonction W de Lambert
Conclusion
La fonction W de Lambert illustre parfaitement comment une découverte mathématique du XVIIIe siècle peut trouver sa véritable utilité pratique près de 250 ans plus tard, grâce aux progrès de l’informatique scientifique. Pour les ingénieurs d’aujourd’hui, elle représente un outil puissant pour résoudre analytiquement des problèmes qui nécessitaient auparavant des méthodes numériques itératives.
Dans le domaine spécifique du calorifugeage industriel, la fonction W de Lambert transforme des calculs d’optimisation complexes en solutions directes et précises, ouvrant la voie à des approches de conception plus efficaces et plus robustes.
Cette redécouverte nous rappelle que les mathématiques recèlent encore de nombreux trésors cachés, attendant simplement le bon contexte technologique pour révéler leur plein potentiel applicatif.
L’auteur remercie les pionniers de la redécouverte moderne de la fonction W de Lambert, dont les travaux ont permis de transformer un outil mathématique abstrait en solution pratique pour l’ingénierie contemporaine.
